Making a ‘mer pass’ observation is one of the simplest, yet most useful navigation tools for sailors to possess, explains Jay Renton
Even day sailors who rarely lose sight of land could enjoy learning the skill to fix a position if your chartplotter or electrical system decides to join the choir eternal.
And for those sailors who find themselves in blue water with terra firma beyond the horizon, making a celestial observation of the sun at meridian passage (aka ‘mer pass’) is one of the simplest, yet most useful navigation tools to possess.

Degrees are found using the scale on the index arm. Minutes are found using the scale on the vernier knob. In this case, the measured sextant angle (SA) is 63° 15.0’
With just a sextant, a chronometer and a nautical almanac, you can get a very good estimate of latitude and a fairly good estimate of longitude.
Taking a night-time observation of Polaris (the North Star) is another straightforward way to determine latitude alone.

Jay Renton had a 20-year career in the United States Air Force. He teaches sextant use and understanding the basics of celestial navigation, and his current project entails the conversion of an old production sloop into a tri-hybrid trawler (see sailingheretic.blogspot.com)
This simplified primer and accompanying pro forma are designed for locations with latitude >23.5°N and westerly longitude.
While this mer pass solar observation is both simple and useful, the big limitation is that the sun must be visible at solar noon.
- The earth rotates through 360° of longitude in 24 hours, so it follows: the earth rotates through 15° of longitude in 1 hour; the earth rotates through 1° of longitude every 4 minutes; the earth rotates through 15’ (a quarter of a degree of longitude) every minute >>> 15° longitude = 1h // 1° longitude = 4m // 15’ longitude = 1m <<<
- The circumference of the earth along any meridian ≈ 21,600nm: 21,600nm / 360° = 60nm / 1° = 60nm / 60’ = 1nm / 1’ >>> 1° latitude = 60nm // 1’ latitude = 1nm <<<
It’s difficult to sail effectively until you know the difference between a sheet and a halyard; likewise, celestial navigation is hard to grasp until you have an understanding of the basic nomenclature:
- Angles are measured using degrees, minutes and tenths of a minute (eg 22° 45.2’). Time is measured in hours and minutes (eg 14h 38m). Please note that ‘minute’ can refer to either an angular quantity or a time quantity.
- Dec/Dec° Declination: the angle measured north or south of the equator, used to describe the GP (geographical position) of a celestial body. The sun’s Dec° varies between 23.5°N (at the summer solstice) and 23.5°S (at the winter solstice), so the hourly change of the sun’s Dec° is quite small. We obtain the sun’s Dec from a nautical almanac. See figure 1, below
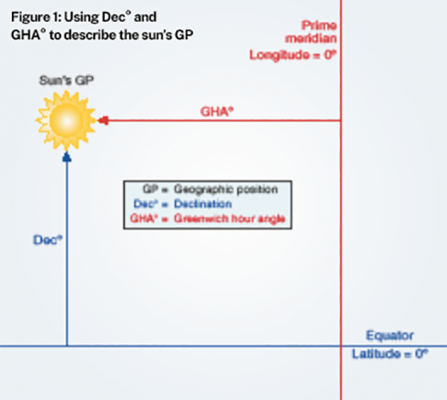
Figure 1
- DR Dead reckoning position: by using magnetic heading, time elapsed and vessel speed, an estimate can be made of the vessel’s position. This DR position is usually not very accurate (due to leeway, tidal currents, etc), but it’s good enough for us to estimate our approximate latitude and longitude, and thus the approximate time of solar noon at our location.
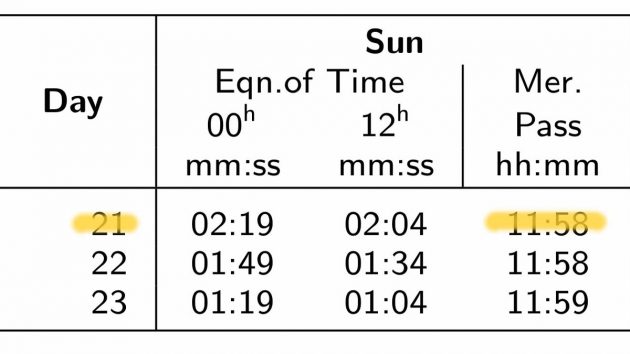
- EOT Equation of time: a method of calculating the difference between mean solar time (and by extension, UTC) and true solar time; they differ by up to 16 minutes throughout the year. This explains why the sun rarely passes the prime meridian at exactly 12:00 UTC.
- GHA/GHA° Greenwich hour angle (GHA): the angle measured west of the Greenwich meridian, used to describe the geographical position (GP) of a celestial body. The sun’s GHA° varies throughout the day between 0° and 360°, so the sun’s GHA° changes quite quickly, about 1° every 4 minutes. It follows that 1° = 60’ (angular) = 4m (time) and 1m (time) = 15’ (angular), so every minute the sun moves through an arc of 15’, or a quarter of a degree. We obtain the sun’s GHA from a nautical almanac. See Figure 1 (above).
- GP We describe the geographical position (GP) of our vessel in terms of latitude and longitude. For our simplified celestial navigation purposes, GP refers to the geographical position of the sun. The sun’s GP is the point on the surface of the earth where the sun is directly overhead; it is constantly changing. We describe the sun’s GP using Dec (Dec = Declination; essentially, the sun’s latitude) and GHA (Greenwich hour angle = essentially, the sun’s longitude). The sun’s Dec changes slowly but its GHA changes quite rapidly. We can find the sun’s GP at any time by using the nautical almanac. See Figure 1 (above).
- Great circle The largest circle that can be drawn on the surface of the earth; the centre of a great circle and the centre of the earth correspond. A great circle divides the earth in two equal hemispheres. Every longitudinal meridian is a great circle. The only circle of latitude that is a great circle is the equator. One minute of arc along any great circle is one nautical mile in length, and one degree of arc is 60nm in length. The shortest distance between any two points on the earth is the path scribed by a great circle.
- He Height of eye: the height of the sextant’s eyepiece above the water when you take an observation; used to determine dip error.
- Ho/Ho° True sextant altitude: Ho° takes observed (raw) SA° and corrects for index error, dip and altitude. The latter two can be determined using the Altitude Correction table (see figure 2 below).
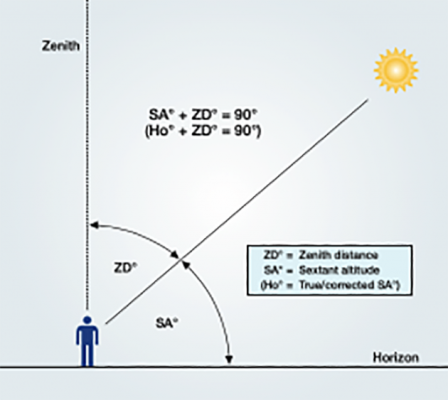
Figure 2: Visual depiction of SA° and ZD°
- Meridian Any line of longitude. The prime meridian is at 0° longitude (Greenwich, England). Our vessel’s local meridian corresponds to our current longitude.
- Mer pass Meridian passage: the point at which the sun passes the local meridian (true south of your position) and has reached its highest point at solar noon. The SA (sextant altitude) will be at its maximum at mer pass. We obtain the time (in UTC) of mer pass at the prime meridian from the nautical almanac and calculate the estimated time of mer pass at our location using our DR longitude (see figure 2 and the pro forma on page 85).
- Nautical twilight The period of time in morning and evening when the centre of the sun is 6°-12° below the horizon; normally it’s dark enough to easily identify a celestial body, yet light enough to easily identify the horizon. Compare with astronomical twilight and civil twilight.
- SA/SA° Sextant altitude: despite its name, SA is actually an angle, not an altitude. SA° is the angle between the sun (or another celestial body) and the horizon; it’s what we measure with the sextant. SA° + ZD° = 90° (see figure 2 above).
- Sextant A device used to very accurately measure the angle between two objects. In our case, we will use it to measure the angle between the bottom edge of the sun (aka, the ‘lower limb’) and the horizon. It can also be used to measure the angular distance between two celestial bodies (eg the moon and a star) or the top of a charted terrestrial feature (like a lighthouse) and the horizon.
- Solar noon The time, anywhere on the earth, at which the sun has reached its highest point, and is located true south (when located north of 23.5°N latitude) on the local meridian. The SA (sextant altitude) of the sun will reach its maximum at solar noon as it passes the local meridian. Mer pass occurs at solar noon.
- UTC Universal coordinated time: also known as GMT (Greenwich mean time), Z (zulu time) and UT (universal time); it’s essentially the mean solar time at 0° longitude. By common agreement, UTC is the time we use anywhere in the world to coordinate the movement of planes and ships, and to synchronise communications, weather forecasts and the observation of celestial bodies. UTC is available at www.utctime.net or by monitoring 10.000 MHz on an HF radio.
- Zenith A line running from the centre of the earth to any point on the surface of the earth, continuing vertically into space. A zenith always makes a 90° angle to the surface of the earth (see figure 2 above).
- ZD/ZD° Zenith distance: despite its name, ZD is actually an angle, not a distance. ZD° is the complement of SA°, ie ZD° + SA° = 90° (see figure 2).
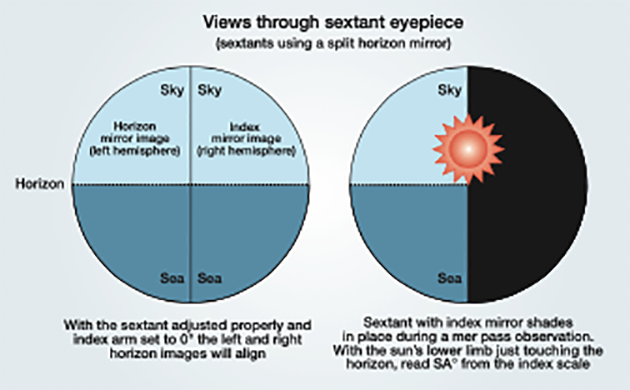
What you’ll see during sextant calibration (left_ and mer pas observation (right)
Celestial navigation: Methodology
Here is the methodology to conduct a mer pass observation of the sun.
This is formalized in the pro forma (opposite) using a sequential, step-by-step format:
- Set your chronometer to UTC. Calibrate the sextant by adjusting the index and horizon mirrors as per the device’s instruction manual.
- Using your DR position, and the nautical almanac, obtain the sun’s Dec and calculate the estimated time (in UTC) of solar noon at your location.
- At 15 minutes before solar noon, begin taking observations of the sun every minute, noting SA° and UTC. Make sure the sextant’s shade lenses are in place before viewing the sun!
- Continue taking observations until the SA° begins to definitely decrease (knowing the direction of true south will help), then determine the UTC of solar noon (aka mer pass) based on the time of maximum SA°; lastly, correct raw SA° for errors (index, dip and altitude) to obtain Ho°, and then calculate ZD° (ZD° = 90° – Ho°).
- Calculate longitude based on the time difference between the UTC of our mer pass (solar noon) and the UTC of mer pass (solar noon) at 0° longitude, knowing that 1 hour of time difference equates to 15° of longitude and 4 minutes of time difference equates to 1° of longitude. Use the Conversion of Arc to Time table, or simply calculate the conversion yourself.
- Calculate latitude using one of the following formulas:
N Dec (North Declination):
Latitude = ZD° + Dec°
or Latitude = (90° – Ho°) + Dec°
S Dec (South Declination):
Latitude = ZD° – Dec° or Latitude = (90° – Ho°) – Dec°
NOTE: This methodology only works for positions north of 23.5°N.
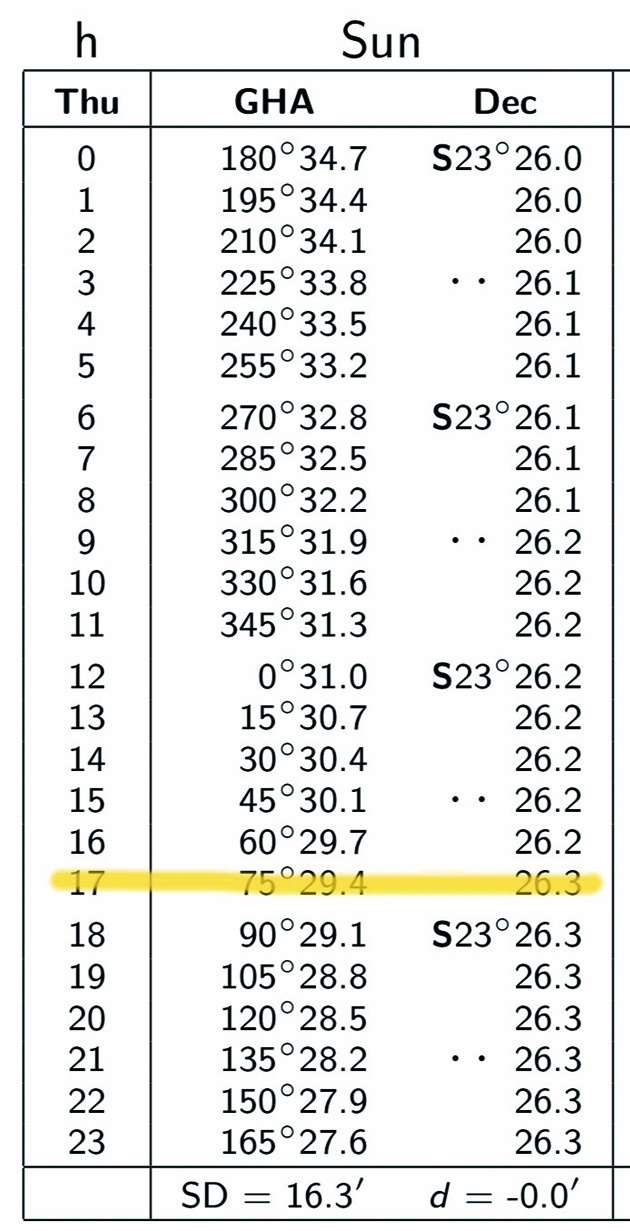
To determine the sun’s GP, find the correct daily page in the nautical almanac then move down to the time desired. Here we see the information for December 21, 2023 at 17:00 UTC. We are most interested in the sun’s declination, which in this case is S 23° 26.3’. As you can see, the sun’s declination changes quite slowly but its GHA changes quite rapidly.

Jay’s sextant is the Davis Instruments Mark 15, available from Amazon or preloved on eBay
The equipment required for this mer pass observation includes:
- Nautical almanac (or sun almanac) for the current year. A full nautical almanac can be downloaded free at TheNauticalAlmanac.com. We are most interested in the sun’s declination and the time of the sun’s meridian passage (mer pass) at the prime meridian (found in the lower right corner of each daily page); it’s a large PDF file best viewed on a tablet. The Conversion of Arc to Time table and the Altitude Correction table for the sun are located at the end of the almanac. NOTE: ‘Sun’ can refer to either the sun (the bright yellow orb in the sky) or as an abbreviation for Sunday.
- Sextant or similar device capable of measuring up to 90° angle equipped with shades/lenses which allow safe viewing of the sun. An octant and quadrant are used in a similar fashion.
- Chronometer. Any digital wristwatch with hh:mm:ss display set to UTC will be accurate enough for our purposes. It might help to also add the ‘UTC’ time zone to your iPhone’s world clock. A UTC time hack can be found at www.utctime.net or tuning to 10.000 MHz on an HF radio.
A great reference for further reading and understanding of celestial navigation is The Practical Guide to Celestial Navigation by Phil Somerville.
Calculating latitude for celestial navigation
A simple way to calculate your latitude (northern hemisphere) using a night/twilight observation
of Polaris:
- Obtain the SA° of Polaris (aka the North Star, aka the Pole Star)
- Correct for index, dip and altitude to obtain Ho° (true sextant altitude)
- Obtain Dec° for Polaris from the nautical almanac
- Use the following formula:
{ Latitude = Dec° – ZD° = Dec° – (90° – Ho°) = Dec° – 90° + Ho° = Dec° + Ho° – 90° } Latitude = Dec° + Ho° – 90° (Polaris, northern hemisphere only) - Since the declination of Polaris is always close to 90° (Dec° ≈ 90°), this can be simplified even further: Latitude ≈ Ho° (your latitude is approximately equal to true sextant altitude)
NOTE: This observation can be taken anytime at night when Polaris is visible, but is most likely to be successful during nautical twilight, when both Polaris and the horizon are easily identifiable.





